¿Hay una mejor forma de contar que la del 1 al 10? Muchos matemáticos creen que sí
Hay un movimiento que aboga por que adoptemos otra manera de contar y tras enterarte de cuáles son sus argumentos quizás te unas a su causa.

Contar es una de las primeras cosas que aprendemos de niños y tanto infantes como adultos muchas veces recurrimos a los dedos de nuestras manos para ayudarnos a calcular números.
El motivo es obvio: tenemos diez dedos, la cantidad exacta de dígitos que existen en nuestro sistema de conteo, el sistema decimal.
De hecho, los antropólogos creen que este sistema surgió justamente por esa razón.
El sistema decimal utiliza diez dígitos: 0 (cero), 1 (uno), 2 (dos), 3 (tres), 4 (cuatro), 5 (cinco), 6 (seis), 7 (siete), 8 (ocho) y 9 (nueve).
A partir de esos se forman todos los números.

Pero aunque nos resulte muy natural, el historiador de Matemáticas Philip Beeley, de la Universidad de Oxford, le contó a la BBC que muchas civilizaciones antiguas usaban un sistema diferente al decimal.
"Si nos remontamos a la Antigüedad clásica tendemos a ver que otros sistemas eran más predominantes", aseguró.
Otras maneras de contar
Algunos ejemplos son el sistema sexagesimal de los Babilonios, que usaba el 60 como base y tenía la tabla trigonométrica más antigua y exacta de la historia.
Si te suena imposiblemente difícil de aplicar recuerda que aún hoy utilizamos este sistema para algunas cosas, principalmente el registro del tiempo: hay 60 segundos en un minuto y 60 minutos en una hora.

Otra sociedades utilizaron una variedad de sistemas. Los Mayas usaban el 20 como base. En tanto, los pueblos antiguos de Estados Unidos y México que hablaban las lenguas chumash usaron el 4.
Incluso hoy, en Papúa Nueva Guinea, hay pueblos nativos que hablan la lengua Kaugel y basan su numeración en el 24.
Pero aunque el sistema decimal logró imponerse en la mayor parte del mundo no todos creen que es el mejor método para contar.
Existe un movimiento que desde la década de 1940 aboga porque se cambie la base de nuestra numeración del diez al... 12.
¿12?
Antes de considerar las ventajas que señalan sus promotores, ¿cómo funcionaría concretamente un sistema duodecimal si sólo tenemos 9 números y el 0?
Para tener 12 dígitos únicos, los promotores del sistema proponen crear dos símbolos más, cuyo lugar estaría después del 9.
Es decir que el 10 se correría dos lugares, y pasaría a valer lo que hoy consideramos 12.

Superado este obstáculo, exploremos la idea.
Los promotores del llamado "sistema docenal" son académicos convencidos de que usar esa base nos facilitaría la vida a todos.
Por un lado, "a los niños les sería más fácil aprender matemáticas", aseguran.
Ponte a pensar: las tablas de multiplicar más fáciles de aprender y recordar son las del 2 y 5.
Eso se debe a que son los números que dividen la base, el 10.
Pero si la base es 12, más tablas de multiplicar serían fáciles de memorizar, algo que reconoce la matemática Vicky Neale, de la Universidad de Oxford, quien antes de ser consultada por la BBC no se había puesto a considerar un cambio de base.

"Hay más que funcionan mejor en base 12 porque hay más números que lo dividen exactamente", le dijo a la BBC.
Efectivamente, las tablas de multiplicar más fáciles de aprender y recordar se duplicarían: las del 2, 3, 4 y 6.
Sin embargo, resaltó Neale, no resuelve todos los problemas.
"Todavía sería difícil dividir por 7", ejemplifica.
La vida cotidiana
Aunque la idea nos resulte inconcebible, sus apóstoles señalan que lo que más se beneficiaría con el cambio son las matemáticas básicas, esas que usamos a diario.
"En un mundo docenal sería mucho más sencillo utilizar el dinero, medir cualquier cosa, calcular un tercio o un cuarto de una cantidad...", le dice a la BBC Stephen Wood, profesor de Física y promotor del sistema.
"El 12 es un número increíble porque puedes dividirlo por dos, por tres, por cuatro y por seis y obtener números enteros", agrega Wood, destacando su más valiosa ventaja: simplifica considerablemente las fracciones.
He aquí un ejemplo visual:
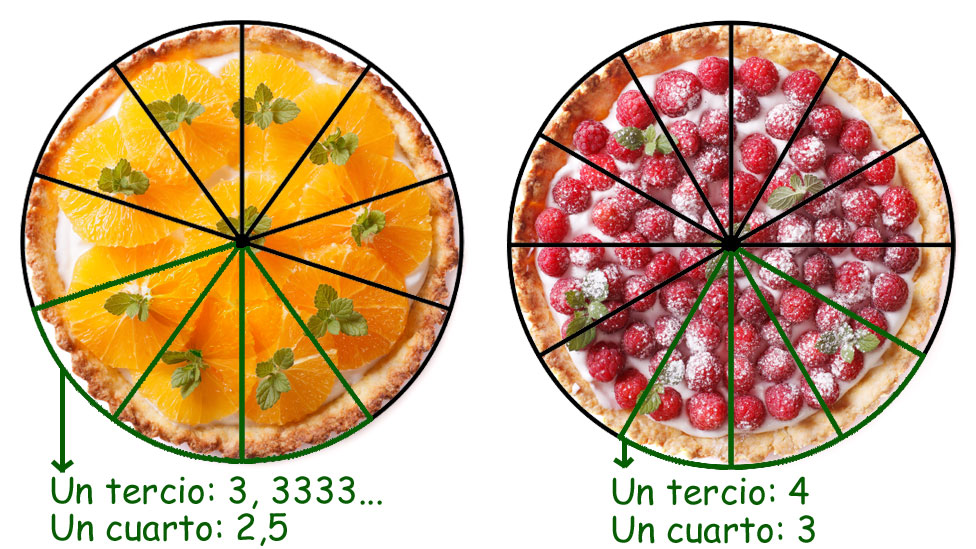
Y mira cómo cuando, por ejemplo, divides 100 con el sistema decimal y el docenal, hay menos fracciones con el último:
Fracciones de 100 | Decimal | Docenal |
|---|---|---|
1 | 100 | 100 |
1/2 | 50 | 60 |
1/3 | 33,3333333333333333333333... | 40 |
1/4 | 25 | 30 |
1/5 | 20 | 24;97... |
1/6 | 16,666 | 20 |
1/7 | 14,285... | 18,6X4 |
1/8 | 12,5 | 16 |
1/9 | 11,1111111111111111111111... | 14 |
1/10 | 10 | 12;497... |
1/11 | 9,09... | 11;11... |
1/12 | 8,333... | 10 |
¿Cambiamos?
Los entusiastas del 12 aseguran que los beneficios superan ampliamente los negativos, y están convencidos de que no sería difícil adoptar el nuevo sistema.
"Las civilizaciones han cambiado de bases aritméticas a lo largo de la historia", señala el físico Wood, quien destaca que incluso hoy conviven varios sistemas que utilizan el 12.

Por ejemplo, para contar los huevos usamos el sistema duodecimal. Y hay 12 pulgadas en cada pie.
También hay otras unidades de medida que siguen siendo muy utilizadas hoy y no se basan en el diez: están las onzas (16 por cada libra), los cuartos (cuatro hacen un galón) y la pinta (que en Reino Unido equivale a 20 onzas y en EE.UU. a 16), entre otras.
Sin embargo, a pesar de sus virtudes, muchos, como la profesora Neale, creen que sería demasiado arduo cambiar de sistema.
"Sería tan confuso para mí y para todos, aunque puedo ver desde el punto de vista matemático... el 12 es un número chévere", concluye.
*Esta es una adaptación del episodio "Is there a better way to count...? 12s anyone?" de BBC Ideas. Si quieres ver el video original haz clic aquí.
Recuerda que puedes recibir notificaciones de BBC News Mundo. Descarga la nueva versión de nuestra app y actívalas para no perderte nuestro mejor contenido.
